Mastering Two-Variable Data and Scatterplots Questions on the SAT

Two-variable data involves examining the relationship between two different types of variables. The number of hours a student studies and their corresponding test scores, the amount of rainfall and crop yield - these are all examples of two-variable data.

On the SAT math section, students are typically required to analyze two-variable data to figure out how changes in one variable might affect the other.

The Scatterplot

One of the most effective methods for visualizing two-variable data is the scatterplot. A scatterplot displays individual data points on a two-dimensional graph, where each axis represents one of the variables. This visual representation helps in identifying patterns, trends, and potential correlations between the variables.

Example Scatterplot

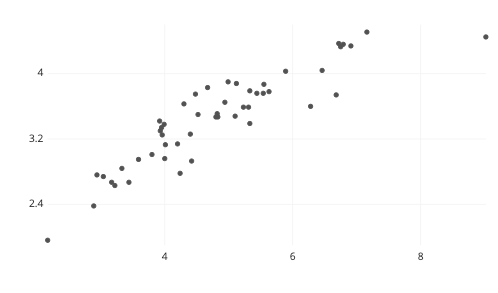
For instance, if we plot study hours on the x-axis and test scores on the y-axis, each point on the scatterplot corresponds to a specific observation, such as a student who studied for a certain number of hours and achieved a particular test score.

By analyzing the scatterplot, we can observe whether there is a positive correlation (both variables increase together), a negative correlation (one variable decreases as the other increases), or no apparent correlation.

Scatterplots are not only useful for visualizing data but also for applying statistical calculations. Students need to beo able to interpret scatterplots, calculate and use the line of best fit, make predictions, and fit various functions to the data. We'll go over each of these skillsets in the following sections.

Line of Best Fit

The line of best fit, also known as a trend line, is a straight line that best represents the data on a scatterplot. It describes the general trend of the data points, making it easier to see patterns and relationships between the variables.

While each data point on the scatterplot represents a specific observation, the line of best fit summarizes these observations with a single line.

The line of best fit can be calculated using statistical methods, but on the SAT, you will often be given the line or asked to draw it approximately. The key here is to ensure that the line minimizes the distance between itself and all the data points.

Once correctly drawn, this line can then be used to interpret the relationship between the variables and make predictions.

Understanding the components of the line of best fit is crucial. The slope of the line indicates the rate of change between the variables. For example, in a study hours versus test scores scatterplot, a positive slope would indicate that test scores tend to increase as study hours increase.

The y-intercept of the line indicates the value of the dependent variable (e.g., test score) when the independent variable (e.g., study hours) is zero.

It's important to note that while the line of best fit can provide valuable insights, it does not imply causation. It merely indicates a correlation between the variables. Therefore, interpreting the slope and y-intercept in the context of the data is essential for drawing meaningful conclusions.

Example Problems

Making Predictions

Using the line of best fit, we can make predictions about the data. If the prediction lies within the range of the data points, it is known as interpolation. If it lies outside the range, it is called extrapolation. These predictions are based on the assumption that the trend indicated by the line of best fit continues.

For example, if our line of best fit for study hours versus test scores is $y = 2x + 50$, we can predict the test score for 5 study hours by substituting 5 for $x$ in the equation. This would give us $y = 2(5) + 50 = 60$.

It's important to remember that predictions are estimates and may not be perfectly accurate. The further the prediction is from the range of the original data, the less reliable it may be. This is because the line of best fit is based on the observed data, and extending it too far beyond this range can lead to inaccurate predictions.

On the SAT, you will often be asked to make predictions based on a given line of best fit. Practice identifying whether you are interpolating or extrapolating and be cautious with predictions that lie far outside the observed data range.

Example Problems

Fitting Functions

On the SAT, you may be asked to fit a function to a scatterplot. These questions are typically multiple-choice and involve identifying the equation that best matches the data trend. The most common types of functions you will encounter are linear and quadratic functions.

For linear functions, you should focus on the slope and y-intercept. The slope indicates the direction and steepness of the line, while the y-intercept indicates where the line crosses the y-axis. To fit a linear function, sketch a line that approximates the data trend and compare its slope and y-intercept with the given choices.

For example, consider the scatterplot below:

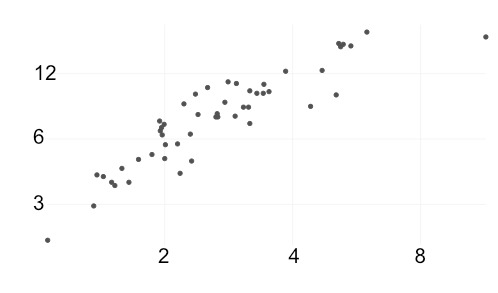
It should be obvious that the data is roughly linear, so we must try to approximate the slope and y-intercept. But first, let's draw the line of best fit:

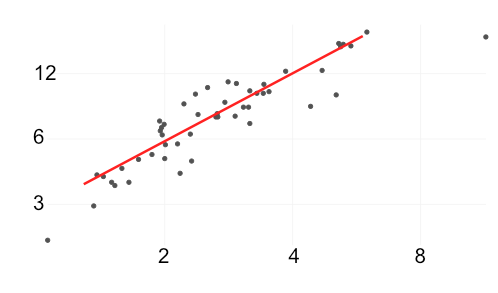
Now, if we try to match the values of the x and y axis markers on the line, we get the points $(2, 6)$ and $(4, 12)$. Using these points, we can find the slope $m$ of the line by using the slope formula $m = \frac{y_2 - y_1}{x_2 - x_1}$. Plugging in the values, we get $m = \frac{12 - 6}{4 - 2} = \frac{6}{2} = 3$.

Next, we use the slope-intercept form of the equation of a line, $y = mx + b$, and plug in one of the points to solve for the y-intercept $b$. Using the point $(2, 6)$, we get $6 = 3(2) + b$, which simplifies to $6 = 6 + b$. Solving for $b$, we find that $b = 0$.

Therefore, the equation of the line is $y = 3x$.

For quadratic functions, consider the direction in which the parabola opens (upward or downward) and its vertex. The vertex is the highest or lowest point of the parabola, depending on its direction. To fit a quadratic function, sketch a parabola that fits the data and identify its vertex and direction.

Practicing these skills will help you quickly identify the correct function on the SAT. Remember to pay close attention to the characteristics of the data trend and match them with the given options.