Mastering Systems of Equations on the SAT

Systems of equations involve two or more equations with two or more variables, and on the SAT you will need to solve systems with two equations and two variables by using the information each equation provides.

Here is an example: $2x + 3y = 12$ and $x - 4y = -2$.

In this system, $x$ and $y$ are the variables, and the goal is to find the values of $x$ and $y$ that satisfy both equations simultaneously.

There are three primary methods to solve a system of equations: Substitution, Elimination, and Graphing. Each method has its advantages, depending on the problem and your preferred solving style.

Substitution

Substitution involves solving one of the equations for one variable and then substituting that expression into the other equation. This method is particularly useful when one of the equations is easy to solve for one of the variables.

By substituting this value into the other equation, we can simplify the system to a single-variable equation, making it easier to solve.

The substitution method is effective when you can easily isolate one of the variables in one of the equations. This often occurs when the coefficient of the variable is 1 or -1. Once you isolate this variable, you substitute it into the other equation, effectively reducing the number of variables and simplifying the problem.

Generally speaking, the substitution method is useful when dealing with equations that are not too complex and when you can quickly solve for one of the variables.

For example, consider the system:
$2y + 3x = 14$
$y - 2x = 0$

Solve the second equation for $y$:
$y = 2x$

Substitute this into the first equation:
$2(2x) + 3x = 14$
$4x + 3x = 14$
$7x = 14 \implies x = 2$

Now, substitute $x = 2$ back into $y = 2x$:
$y = 2(2) = 4$

So, $x = 2$ and $y = 4$.

Example Problems

Elimination

Elimination involves adding or subtracting equations to eliminate one of the variables. This method is effective when both equations are in standard form and it’s easy to align the coefficients of one of the variables.

By manipulating the equations, you can add or subtract them to cancel out one variable, reducing the system to a single-variable equation.

The elimination method is particularly powerful when the coefficients of one of the variables are already or can easily be made equal. By multiplying one or both of the equations by suitable numbers, you can align the coefficients.

Then, you either add or subtract the equations to eliminate that variable, simplifying the problem to a single-variable equation. This method is efficient for systems where aligning the coefficients is straightforward and avoids the complexity of fractions in the early stages of solving.

For example, consider the system:

$2y + 4x = 20$
$y - x = 1$

Multiply the second equation by 2 to align the $y$ terms:
$2(y - x = 1) \implies 2y - 2x = 2$

Now we have:

$2y + 4x = 20$
$2y - 2x = 2$

Subtract the second equation from the first:

$(2y + 4x) - (2y - 2x) = 20 - 2$
$6x = 18 \implies x = 3$

Substitute $x = 3$ into the first equation to find $y$:
$2y + 4(3) = 20 \implies 2y + 12 = 20 \implies 2y = 8 \implies y = 4$

So, $x = 2$ and $y = 16$.

Elimination is particularly useful when both equations are in standard form and the coefficients of one of the variables are already close in value or can be easily manipulated to become equal. This method avoids dealing with fractions early in the solution process.

One of the key advantages of the elimination method is its applicability to more complex systems with higher coefficients. It provides a systematic approach that is less prone to errors from fraction manipulation compared to substitution.

Example Problems

Graphing

Graphing involves plotting each equation on the same set of axes and finding their intersection point, which represents the solution to the system. This method is particularly visual and is useful when you want to understand the relationship between the equations. It’s especially effective when the equations are in slope-intercept form or can be easily converted into it.

The graphing method provides a clear visual representation of the solutions to the system of equations. By plotting the equations on a coordinate plane, you can see where the lines intersect, which represents the solution to the system. This method is particularly useful for understanding the geometric relationship between the equations and is helpful in identifying the number of solutions (one, none, or infinitely many). It is also beneficial for verifying solutions obtained through other methods.

For example, consider the system:

$2y + 4x = 20$
$y - x = 1$

Convert each to slope-intercept form:

$2y = -4x + 20 \implies y = -2x + 10$
$y = x + 1$

Graph these equations and find the intersection point.

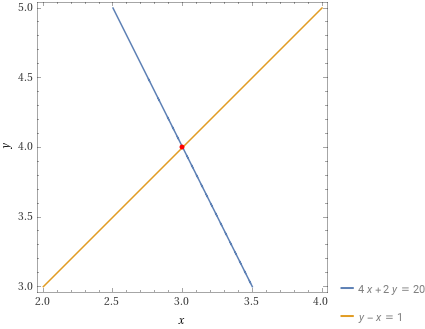
The intersection point is $(3, 4)$, so $x = 3$ and $y = 4$.

Graphing is most effective when you need a visual representation of the solution or when the equations are already in or can be easily transformed into slope-intercept form. This method is also helpful for verifying solutions found by other methods.

One of the advantages of the graphing method is its ability to handle systems where the equations are not easily manipulated algebraically. It provides a straightforward approach for identifying solutions when the equations are complex or involve higher-order terms.

Additionally, graphing can help in understanding the nature of the solutions, such as whether the lines intersect, are parallel, or are coincident.

While graphing is a powerful tool, it is less reliable as small errors in graphing can lead to incorrect solutions. Therefore, it is often used in conjunction with other methods to confirm the accuracy of the solutions. Be sure to sanity-check your answers when using the graphing method.

Extra Practice Questions